Adding binary Numbers
A key requirement of digital computers is the ability to use logical functions to perform arithmetic operations. the basic of this addition if we can add two binary numbers, we can just as easily subtract them, or get a little function and perform multiplication and division. How,then,do we add two binary numbers? Lets start by adding two binary bits. since each bit has only two possible values,0 or 1 , there are only four possible combinations of inputs. these four possibilities, and and the resulting sums, are:
 |
| (this image about adding binary number from creatingmm.com) |
That fourth Line indicates that we have to account for two output bits when we add two input bits: the sum and a possible carry. Let's set this up as a truth table with two inputs and two outputs, and see there we can go from there.
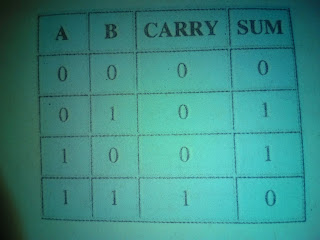 |
| (this image about adding binary number from creatingmm.com) |
Well this look familiar, does't it? the carry output is a simple AND function, and the sum is an Exclusive-OR Thus, We can use two gates to add these two bits together. The resulting circuit is shown below
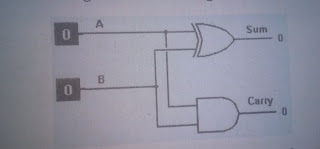 |
| (this image is about adding binary number by creatingmm.com) |
Ok we have got a good start on this circuit, However, We're not done yet. in a computer, we'll have to add multi-bit numbers together. if search pair of bits can produce an output carry, it must also be able to recognize and include a carry from one column to the next, the next column has same requirement as adding decimal numbers-if you have a carry from one column to the next, the next column has to include that carry. We have to do the same thing with binary numbers, for the same reason. As a result, the circuit to the left is known as a "half adder," because it only does half of the job. We need a circuit that will do the entire job. to construct a full adder circuit, we'll need three inputs and two outputs. since we'll have the final sum output. the resulting truth table is shown below. the resulting full adder circuit is shown below.
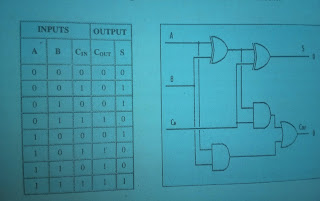 |
| (this image is about adding binary number by creatingmm.com) |
Negative Numbers and Binary Subtraction
We have seen how simple logic gates can perform the process of binary addition. it is only logical to assume that a similar circuit could perform binary subtraction. if we look at the possibilities involved in subtracting one 1-bit number from another, we can quickly see that three of the four possible combinations are easy and straight-forward. the fourth one involves a bit more:
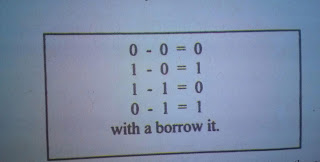 |
| (this image is about binary subtraction from creatingmm.com) |
That borrow bit is just like a borrow in decimal subtraction: it subtracts from the next higher order of magnitude in the overall number. Let's see what the truth table look loke. this is an interesting result. the difference, A-B, still an Exclusive-OR function, just as the sum was for addition. the borrow is still an AND function, but is A'B instead of AB
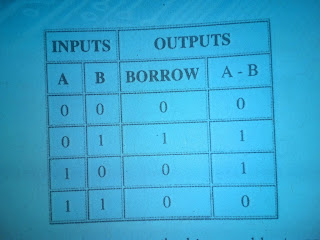 |
| (this image is about binary subtraction by the creatingmm.com) |
What we'd like to do. now, is fined an easy way to use the binary adder to perform subtraction as well. we already have half of it working: the difference output. Can we simple invert the A input so the AND gate will have the right signals? No, we can't because that would invert the sense of the Exclusive-OR function.
What would be really nice is to convert B to the negative of any number, we can convert our original 4-bit adder circuit to an adder/subtractor. by leaving the inputs unchanged, we get the result of A+B . But if we invert B and add 1 with the low-order CIN, we get the result of A-B
Some Advance Tips
If you like this article so please share this post , and if you know to interest about RAM, ROM, and PC so visit my site : https://www.digitaltech.net.in
No comments:
Post a Comment